10 Shear Loads
Introduction
Click to expand
In Chapter 9 we learned to calculate bending stresses in beams and how to design beams to resist bending stress. The transverse loading applied to beams will also create internal shear loads and therefore shear stresses that must be calculated and accounted for (Figure 10.1).
In this chapter, we’ll first review an important geometric property known as the first moment of area and demonstrate how to calculate it for common beam cross-sections in Section 10.1. In Section 10.2 we’ll discuss shear stresses in beams and how to calculate them. In Section 10.3 we’ll discuss shear flow, which is useful for beams with cross-sections formed by joining two or more parts with fasteners such as nails.
10.1 The First Moment of Area
Click to expand
Shear stress in an object depends on the internal shear force and the shape of the cross-section. One important geometric property used in this chapter is the first moment of area. This property was introduced in Section 8.1 and was used when determining the centroid of an area. Recall we used @eqn-8.2 to break simple cross-sections down into a number of composite parts. When finding the centroid of these composite areas we modified the equation slightly to:
\[ \bar{y}=\frac{\sum y_i A_i}{\sum A_i}=\frac{y_1 A_1+y_2 A_2+\ldots}{A_1+A_2+\ldots} \]
We can rewrite this equation in its integral form:
\[ \bar{y}=\frac{\int y d A}{\int d A} \]
The numerator in this equation is the first moment of area. It will be given the symbol Q.
\[ Q=\int y d A \]
Similarly, for the purposes of this text we can write:
\[ \boxed{Q=\sum y_i A_i=y_1 A_1+y_2 A_2+\ldots} \tag{10.1}\]
Q = First moment of area [m3, in.3]
y = Vertical distance from neutral axis to centroid of area A [m, in.]
A = Area above (or below) point of interest [m2, in.2]
In Section 8.1 we performed this calculation relative to some convenient reference axis in order to determine the location of the centroid of an area (such as in Example 8.3). Ai represents the area of each composite part and yi represents the distance from the reference axis to the centroid of each composite part.
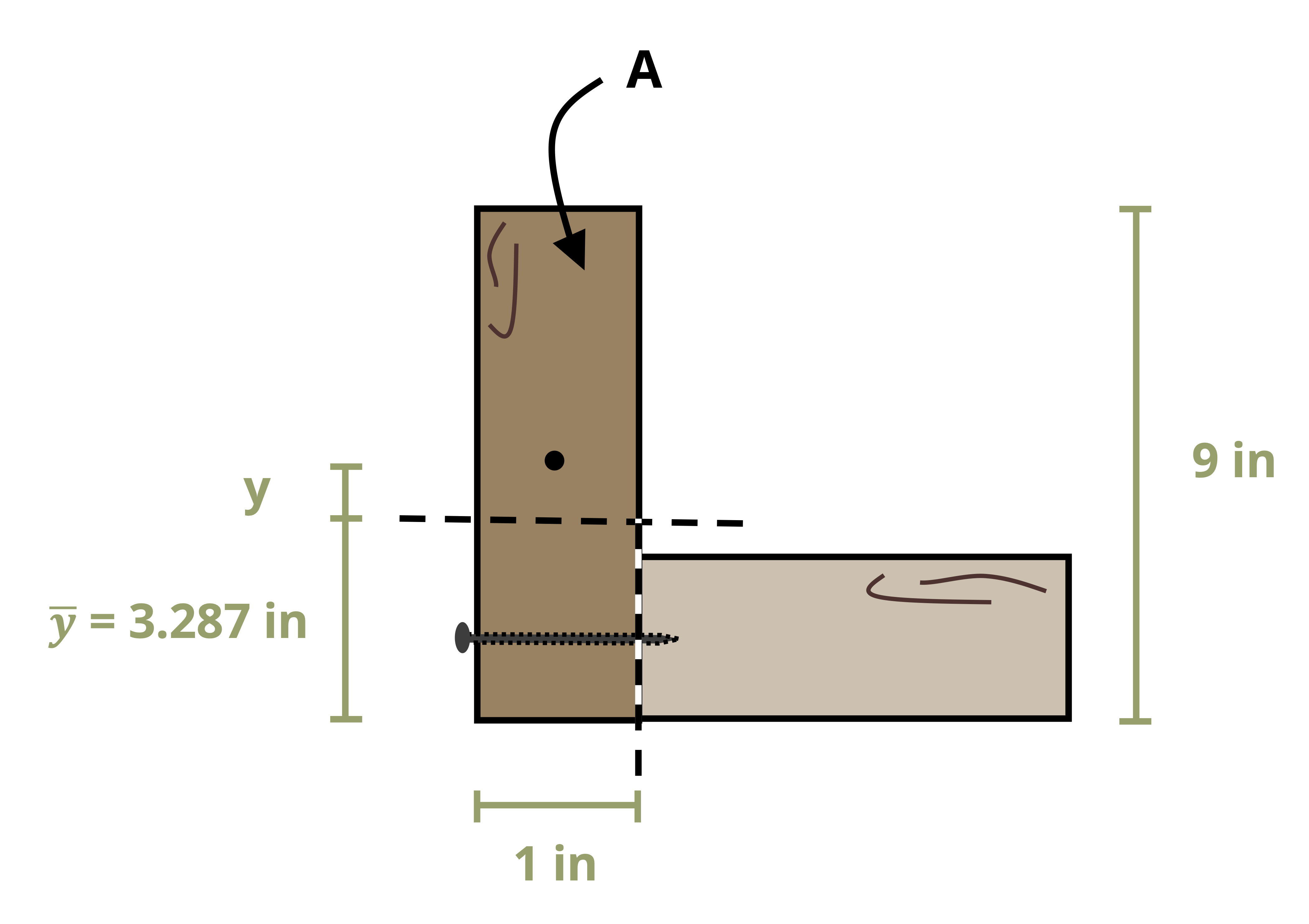
The first moment of area can actually be calculated around any axis. The maximum value will always occur at the centroid of the cross-section (i.e., the neutral axis) so many problems will involve finding the first moment of area at the neutral axis, but there are also cases where finding the first moment of area around some other axis is required. Note that the axis should be perpendicular to the shear force, so a vertical load requires us to use a horizontal axis.
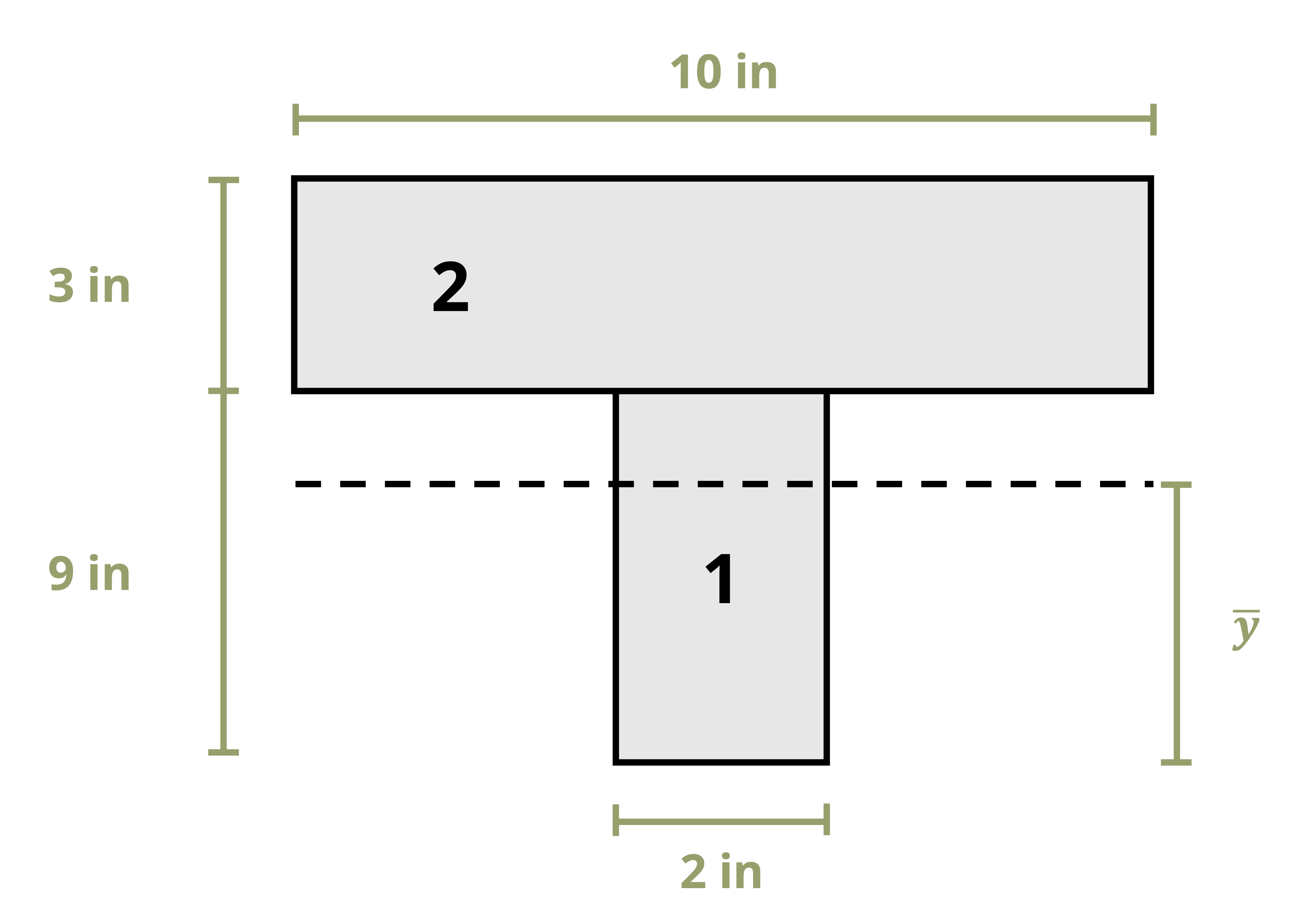
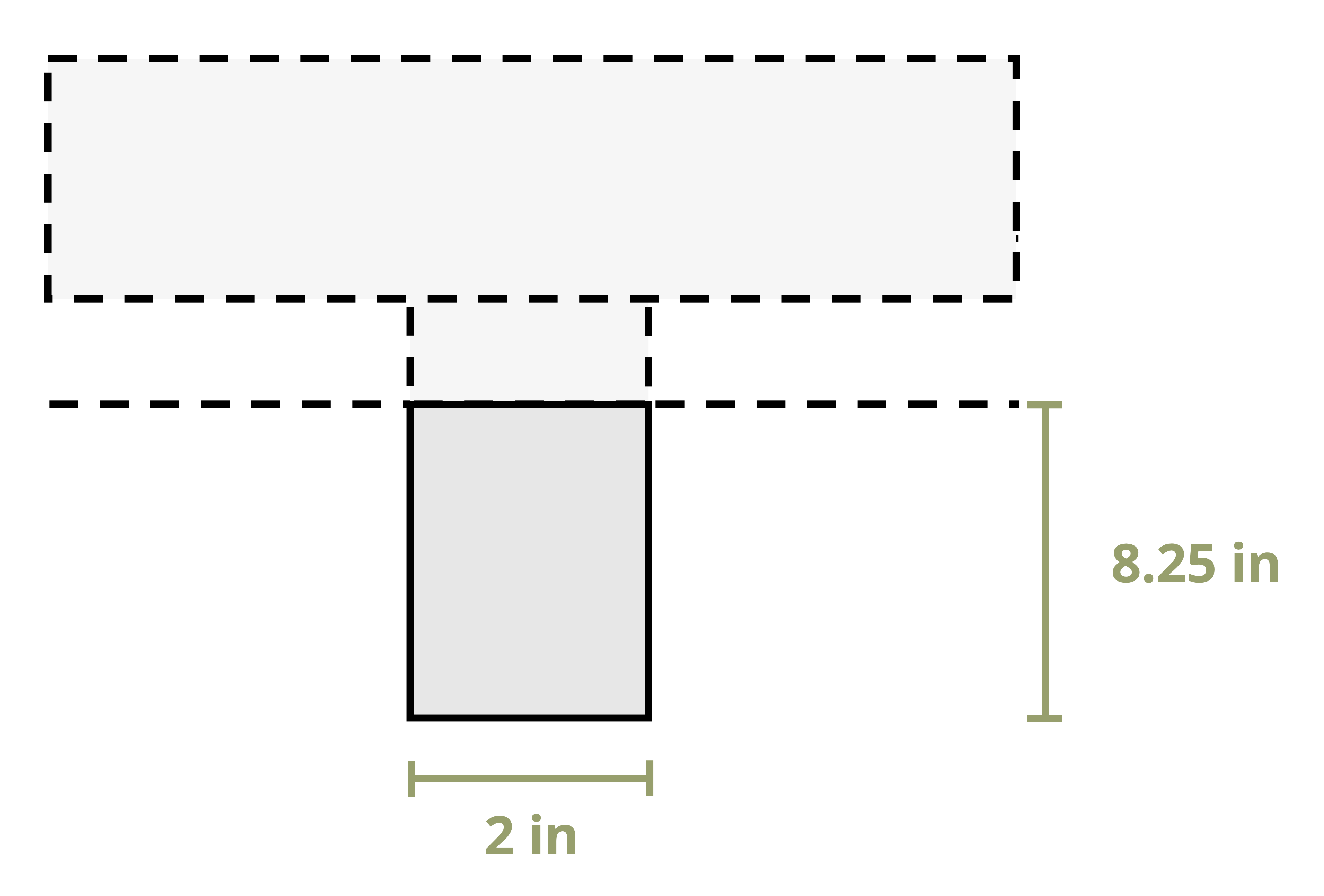
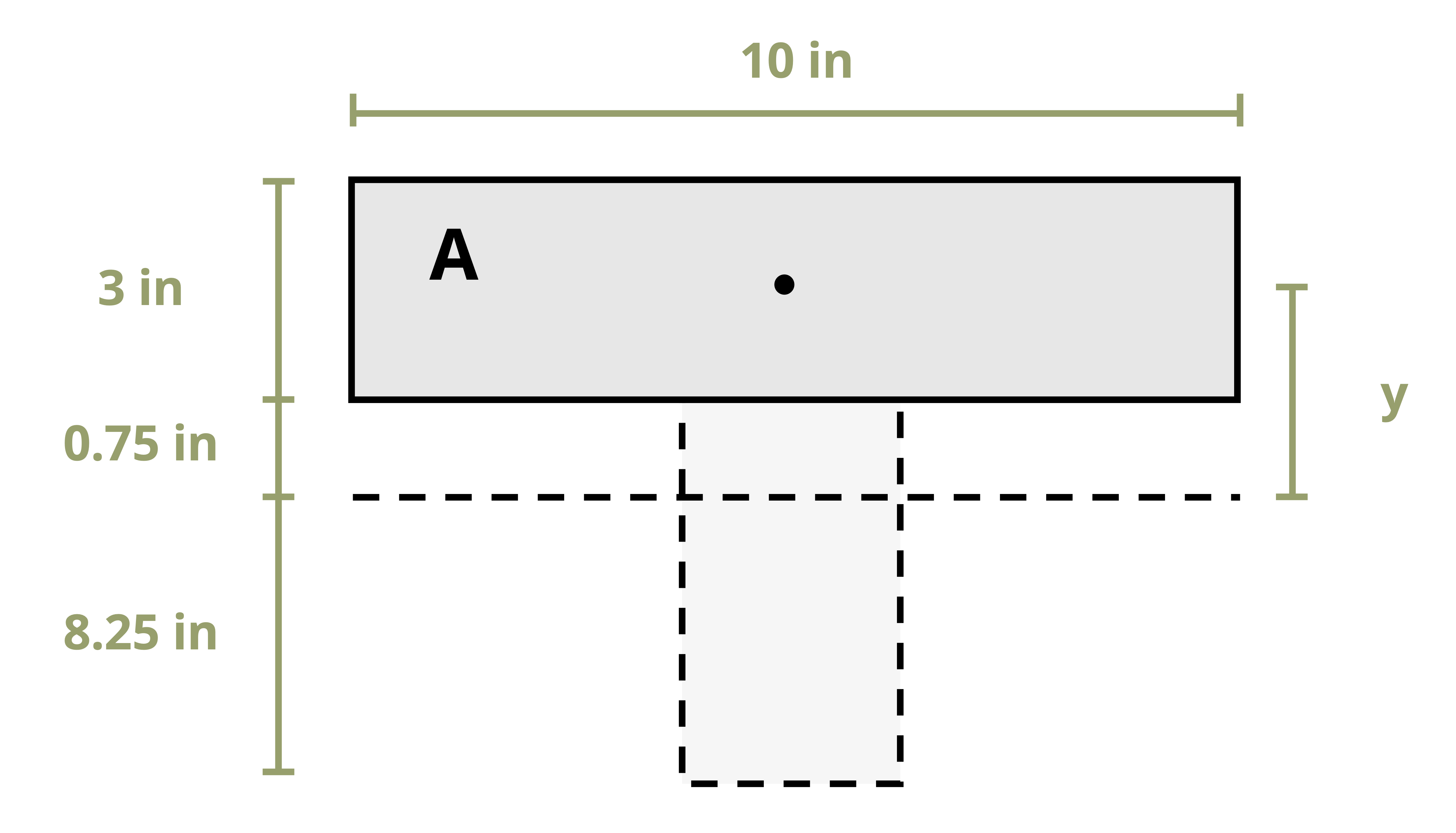
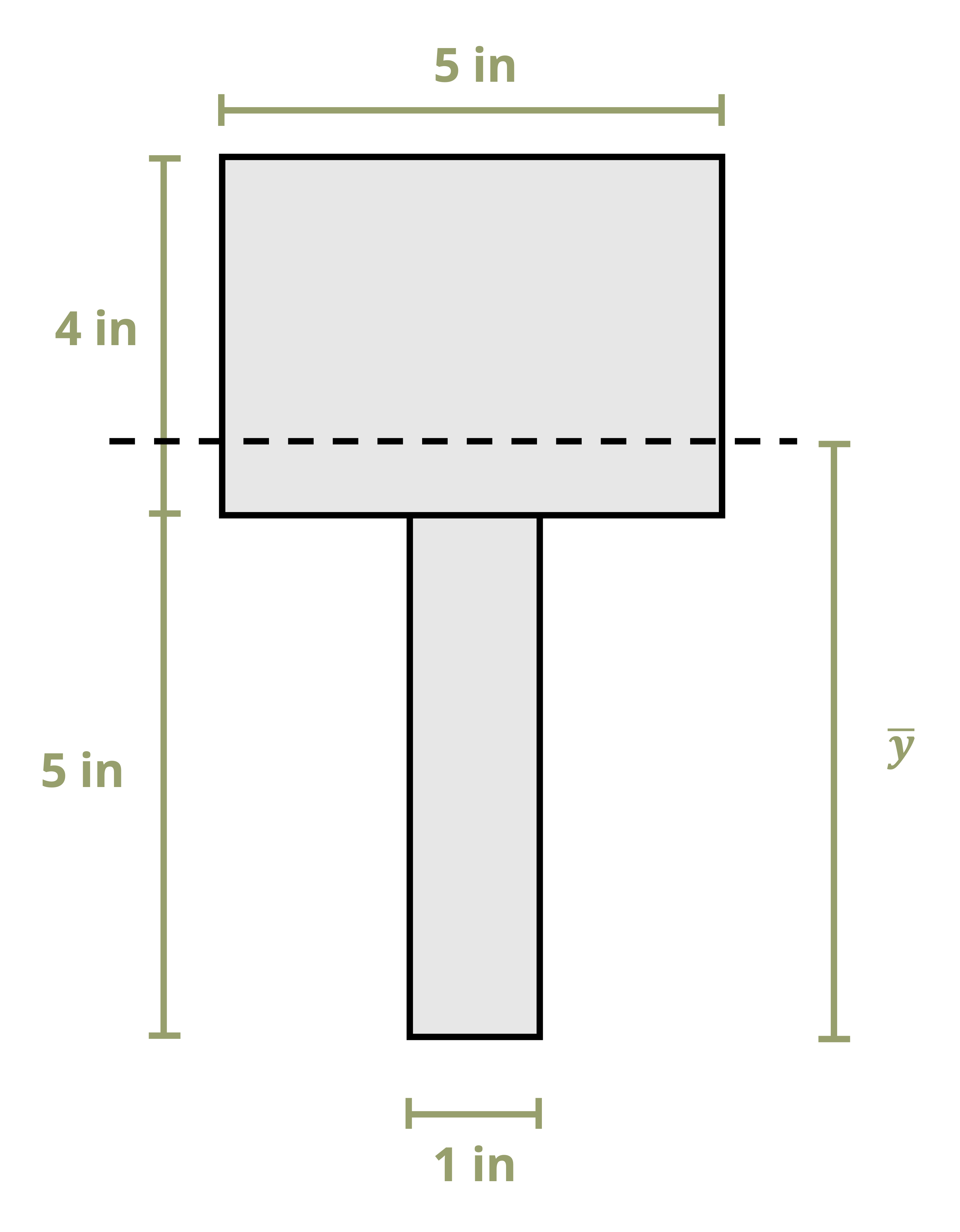
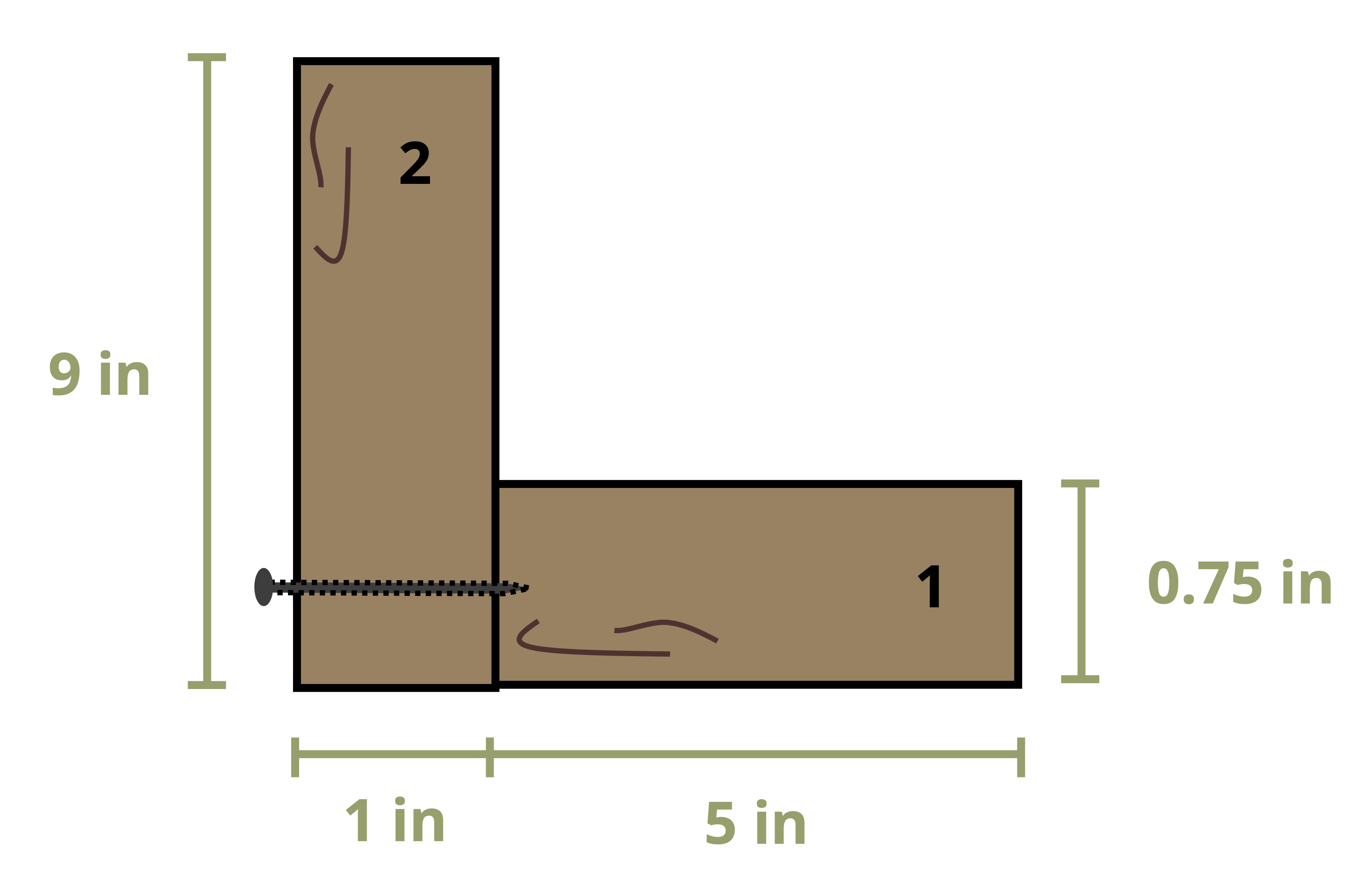
To calculate the first moment of area around an axis, first draw a line through this axis. We may choose to use either the area above this axis or the area below it, whichever is simpler. The answer will be the same either way. Break this area down into composite parts (if necessary) and apply \(Q=\sum y_i A_i\) where Ai is the area of each composite part and yi is the perpendicular distance between the centroid of the overall cross-section and the centroid of each composite part. Note that we must first find the location of the centroid of the overall cross-section in order to measure this distance.
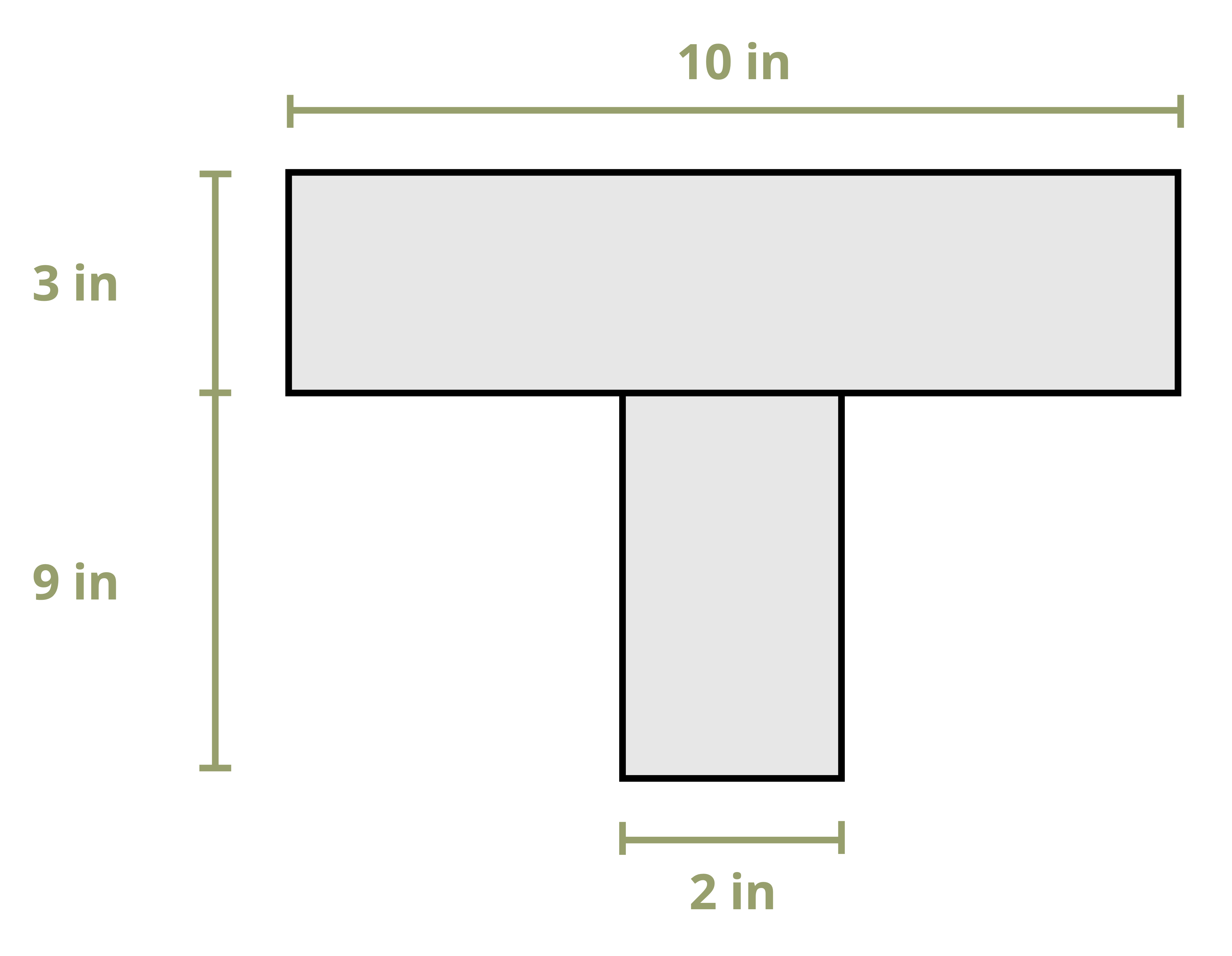
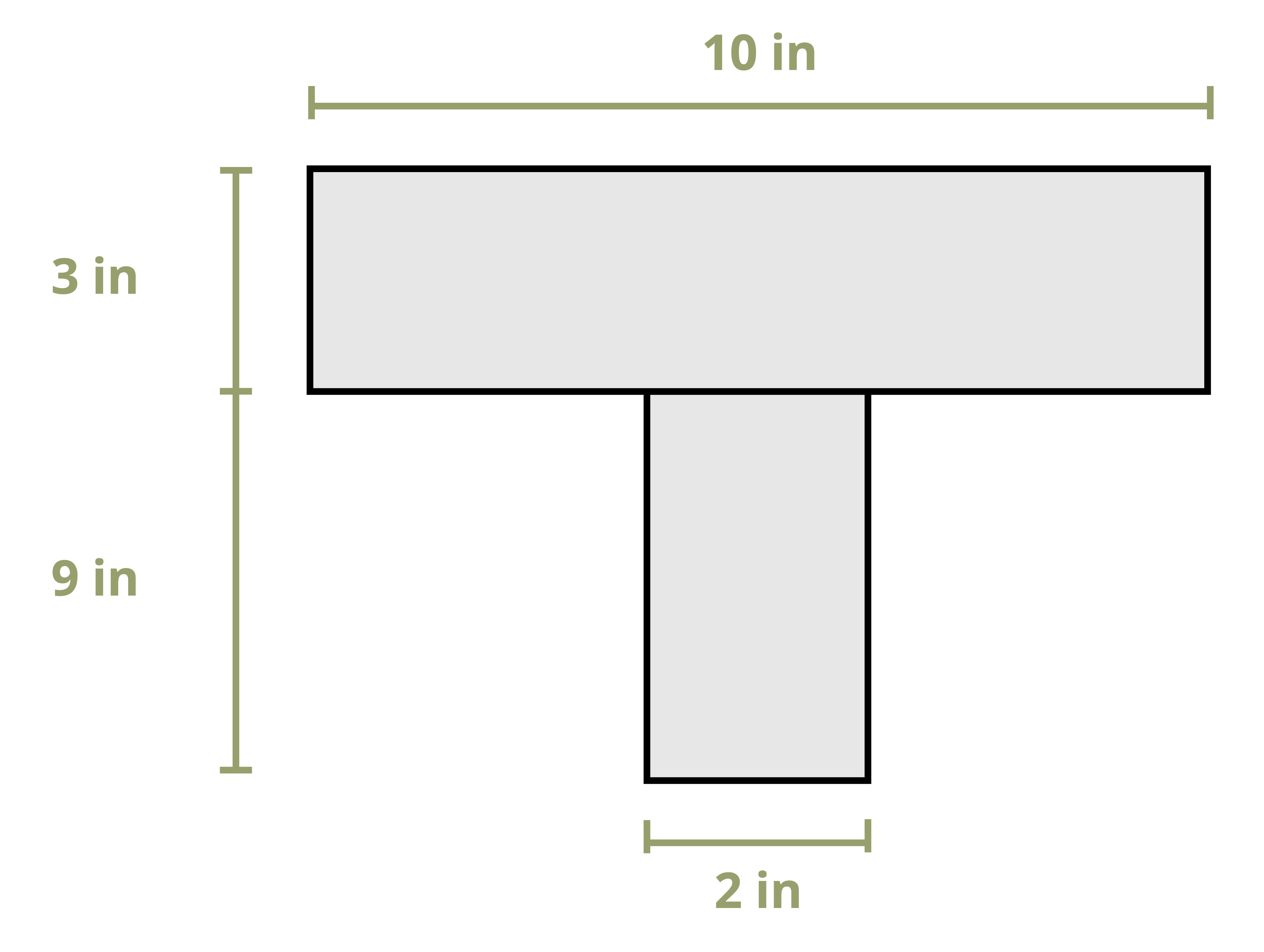
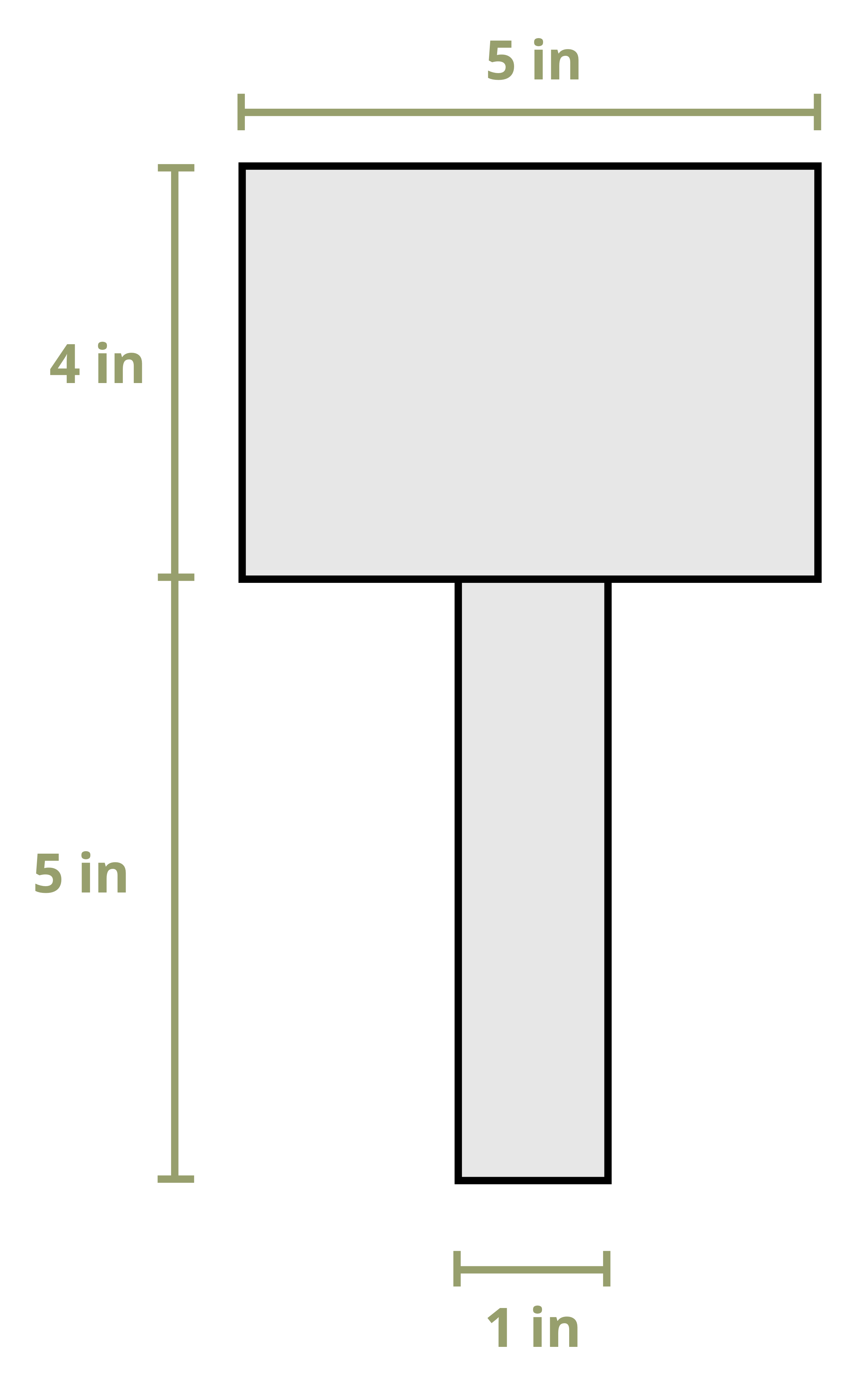
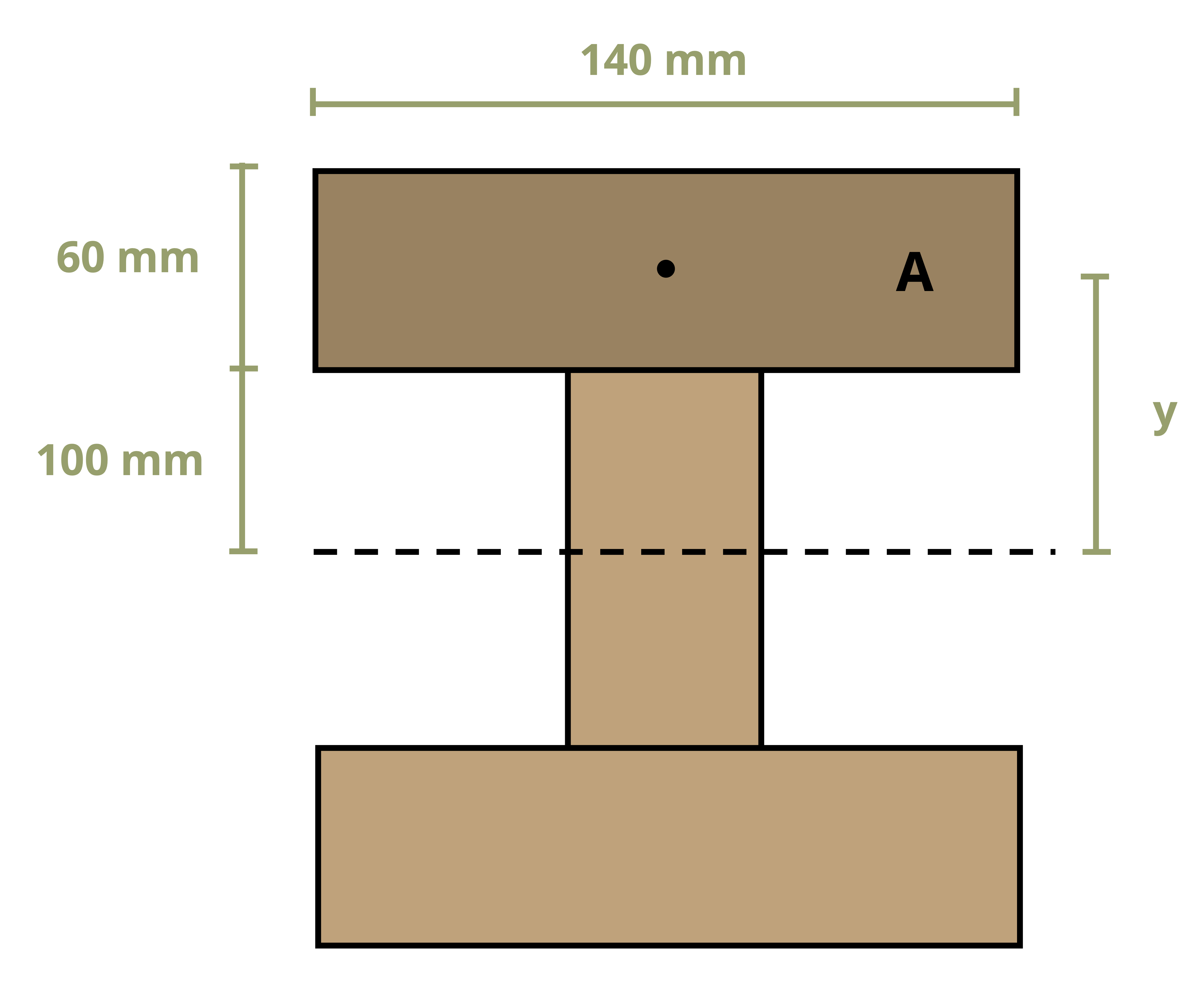
Example 10.1 demonstrates this process to find the first moment of area around the neutral axis of a T cross-section. This example is solved twice, once using the area below the neutral axis and once using the area above.
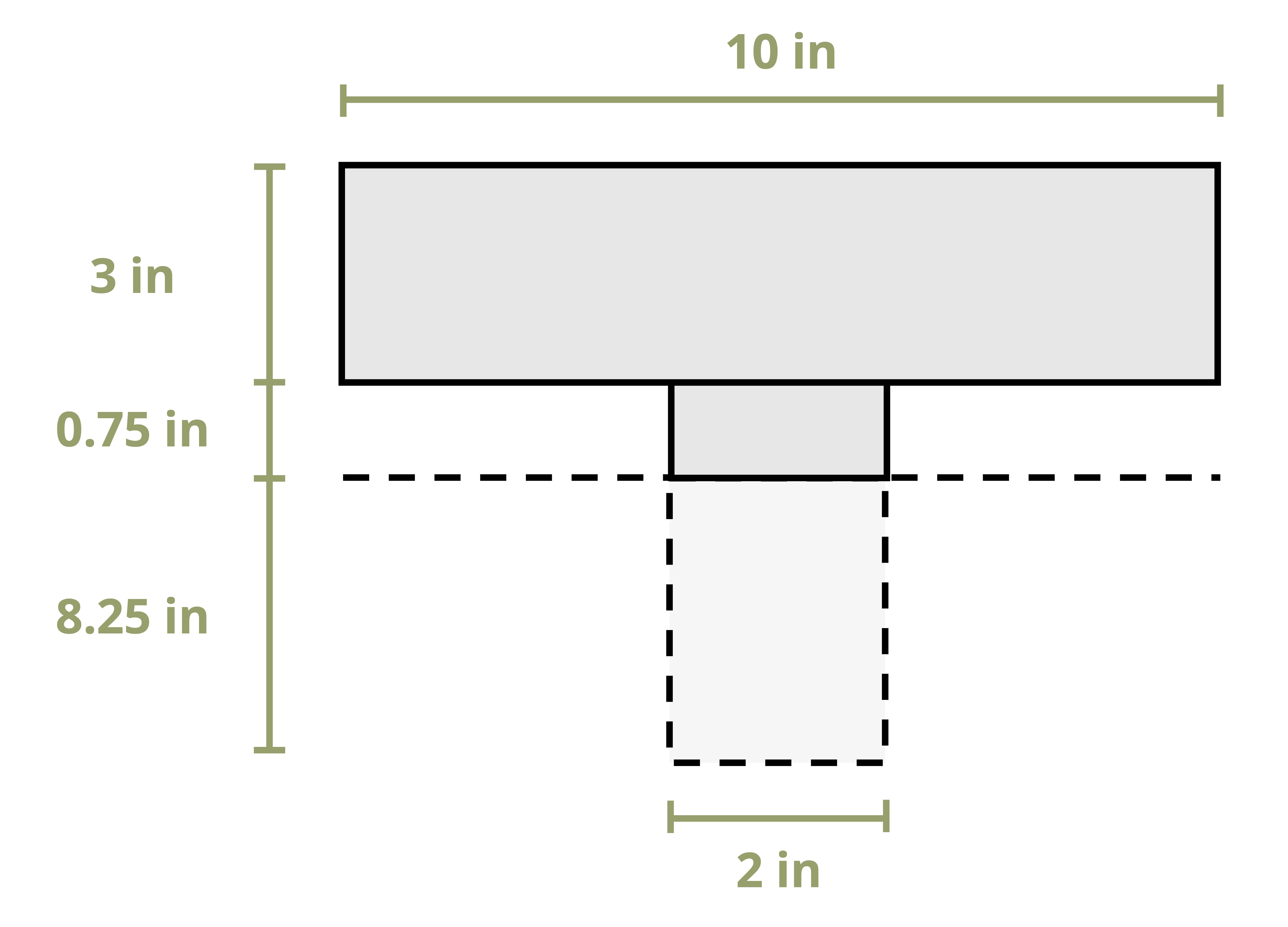
Example 10.2 uses the same cross-section and demonstrates calculating the first moment of area around a different axis on the cross-section.
Example 10.1
A beam has the T-shaped cross-section shown. Determine the first moment of area around the neutral axis of the cross-section.
First determine the y-coordinate of the centroid of the cross-section. Consider the area as two rectangles and use the method of Section 8.1. We will choose a reference point at the bottom of the section to calculate the centroid.
\[ \begin{aligned} & y_1=4.5{~in.}~,~ A_1=18{~in.}^2 \\ & y_2=10.5{~in.}~,~ A_2=30{~in.}^2 \\ & \bar{y}=\frac{(4.5{~in.} * 18{~in.}^2)+(10.5{~in.} * 30{~in.}^2)}{18{~in.}^2+30{~in.}^2}=8.25{~in.}~~\text{from the bottom of the section (our reference point) } \end{aligned} \]
Note that since this section is simple, only two shapes, we didn’t create a table as we did in Section 8.1. This is a simplified version of the table, but the calculation is exactly the same.
Now draw a horizontal line through the point of interest. In this case the point of interest is the neutral axis. Use either the area above this line or the area below this line to determine the first moment of area around the neutral axis. We’ll solve it both ways to demonstrate that we get the same answer either way.
Area below the neutral axis:
This area is a simple rectangle. Recall that Q=yA where A is the area of the rectangle and y is the vertical distance between the neutral axis and the centroid of the rectangle.
\[ \begin{aligned} & y=\frac{8.25{~in.}}{2}=4.125{~in.} \\ & A=8.25{~in.} * 2{~in.}=16.5{~in} ^2 \\ & Q=y A=4.125{~in.} * 16.5{~in.}^2=68.1{~in.}^3 \end{aligned} \]
Area above the neutral axis:
This area can be split into two rectangles. Here we’ll use \(Q=\sum y_i A_i=y_1 A_1+y_2 A_2\)
\[ \begin{aligned} & y_1=\frac{0.75{~in.}}{2}=0.375{~in.} \\ & A_1=0.75{~in.} * 2{~in.}=1.5{~in.}^2 \\ & y_2=0.75{~in.}+1.5{~in.}=2.25{~in.} \\ & A_2=10{~in.} * 3{~in.}=30{~in.}^2 \\ & Q=(0.375{~in.} * 1.5{~in.}^2)+(2.25{~in.} * 30{~in.}^2)=68.1{~in}^3 \end{aligned} \]
Whether we use the area above the neutral axis or the area below the neutral axis, we get the same answer of Q=68.1 in3. We may choose to use whichever area seems simpler to work with.
Example 10.2
The T-shaped cross-section from Example 10.1 is repeated here. Determine the first moment of area around an axis passing through the interface between the flange and web.
We need to first determine the y-coordinate of the centroid of the cross section. We did this in Example 10.1, the results are shown below.
\(\bar{y}=8.25{~in.}\) from the bottom of the cross-section.
Now draw a horizontal line through the point of interest. In this case the point of interest is the seam between the two boards. As demonstrated in Example 10.1, we may use either the area below this line or the area above this line to determine the first moment of area.
Area above the line:
This area is a simple rectangle. Recall that Q=yA where A is the area of the rectangle and y is the vertical distance between the neutral axis and the centroid of the rectangle. Note that the perpendicular distance is always measured to the neutral axis, not to the seam between the two boards.
\[ \begin{aligned} & y=0.75{~in.}+1.5{~in.}=2.25{~in.} \\ & A=10{~in.} * 3{~in.}=30{~in.}^2 \\ & Q=y A=2.25{~in.} * 30{~in.}^2=67.5{~in.}^3 \end{aligned} \]
As an additional exercise, try using the area below the seam between the two boards to calculate Q=67.5 in.3.
Simple cross-sections such as rectangles and circles are fairly commonly used for beams. For these simple cross-sections we can derive standard solutions for the maximum first moment of area (Qmax). Recall that this always occurs at the neutral axis of the cross-section.
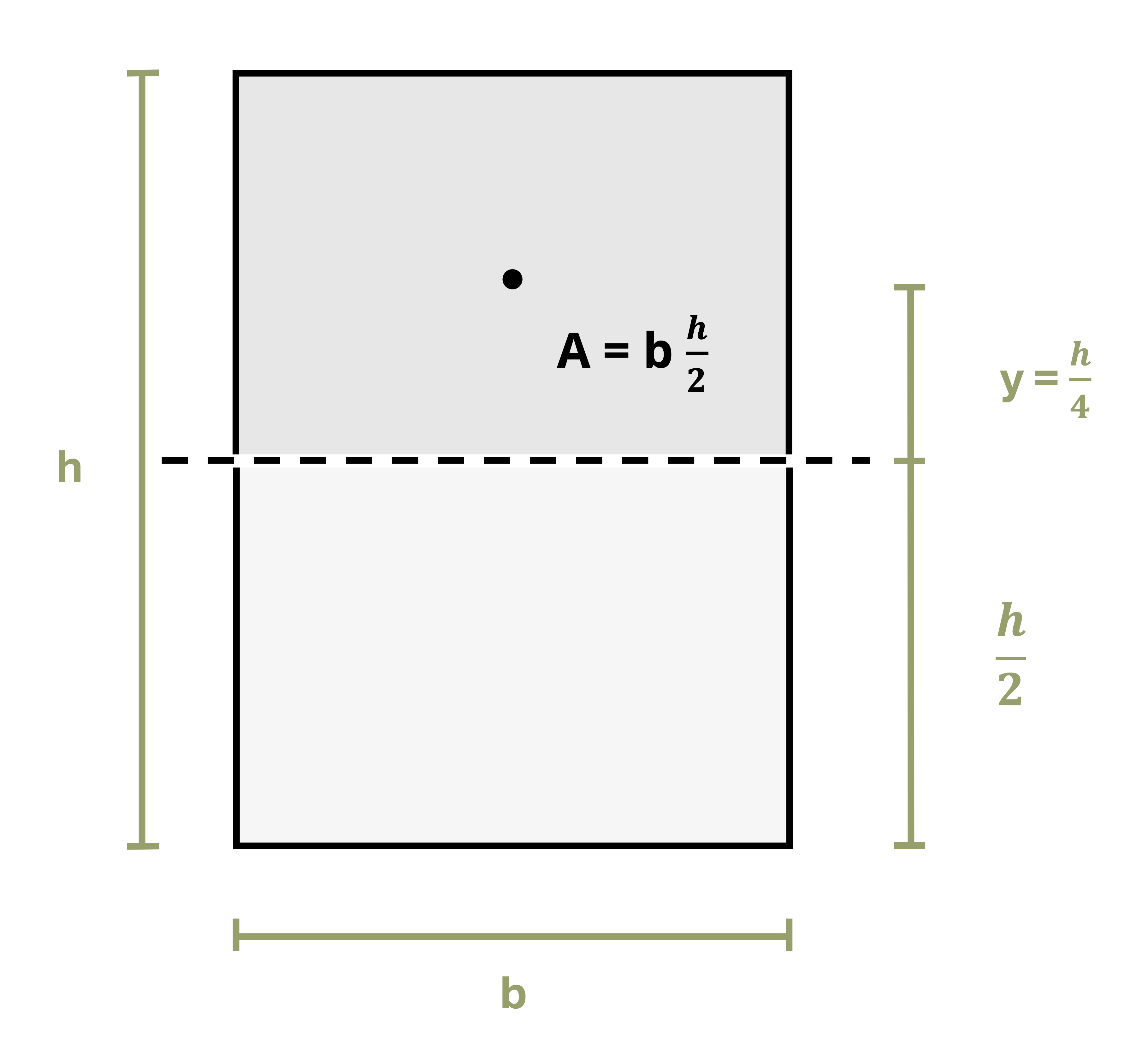
For a rectangle of base b and height h (Figure 10.2), the neutral axis will be at \(y=\frac{h}{2}\). Drawing a line along the neutral axis and taking the area above this line gives \(A=b \frac{h}{2}\). The distance between the centroid of this area and the neutral axis of the cross-section will be \(y=\frac{h}{4}\). Thus, for a rectangular cross-section:
\[ Q_{\max }=\frac{h}{4} \frac{b h}{2}=\frac{b h^2}{8} \]
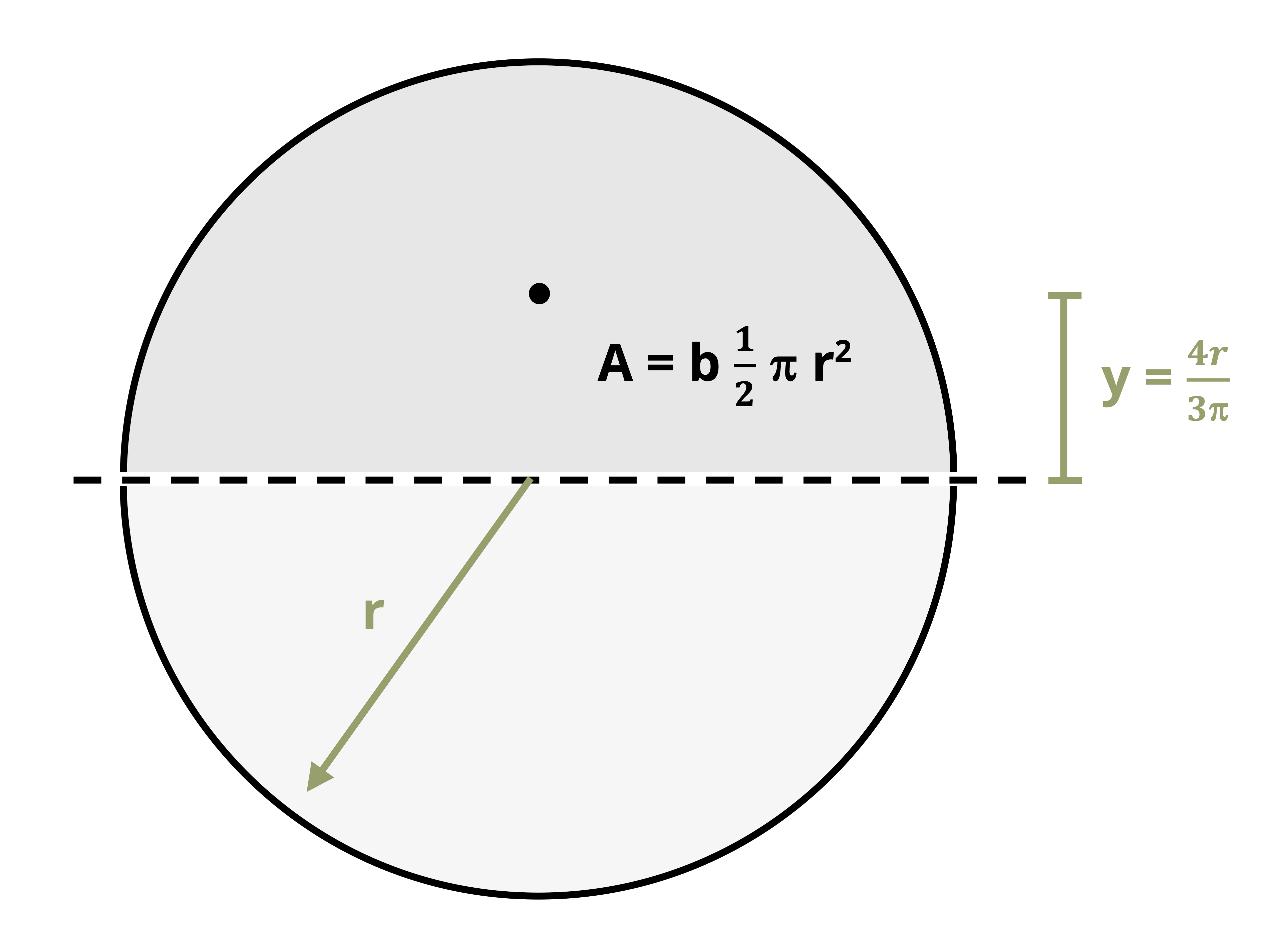
For a circular cross-section of radius r (Figure 10.3), the area above the neutral axis is semi-circle so \(A=\frac{1}{2} \pi r^2\). The distance from the centroid of the semi-circle to the neutral axis is \(y=\frac{4 r}{3 \pi}\). Thus, for a circular cross-section:
\[ Q_{\max }=\frac{4 r}{3 \pi} \frac{1}{2} \pi r^2=\frac{2}{3} r^3 \]
Note that both of these are only for finding the first moment of area at the neutral axis (Qmax). If the first moment of area around any other axis is required, these shortcuts will not work, and the general process will need to be used.
10.2 Shear Stress
Click to expand
In Section 2.2 we learned about average shear stress:
\[ \tau_{avg}=\frac{V}{A} \]
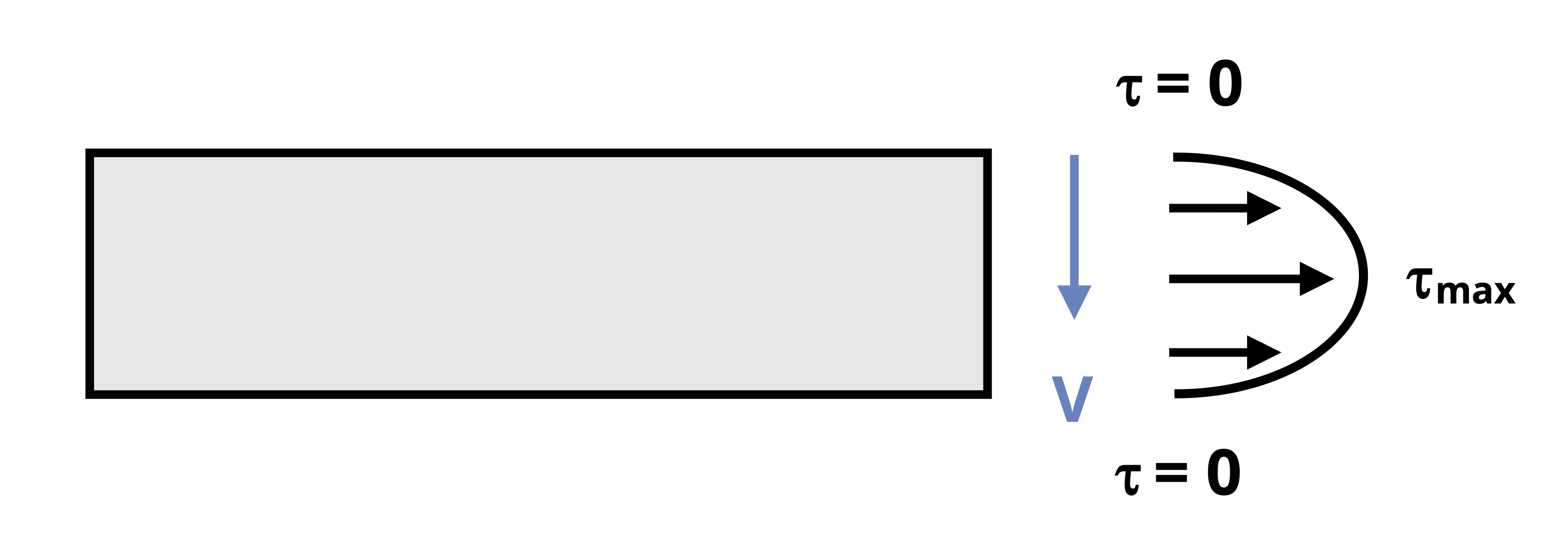
This is the average shear stress on a cross-section, but shear stress actually varies along the section (Figure 10.4). For a vertical internal shear force, shear stress is zero at the top and bottom of a cross-section and maximum at the neutral axis. Shear stress varies in a parabolic fashion. The average shear stress does not provide a full picture and it is often necessary to calculate the shear stress at a specific point on the cross-section instead.
To derive the shear stress formula, we’ll begin by examining a small 2D element on a body subjected to an internal shear force (Figure 10.5). If this element is in equilibrium, a shear force applied to one face of this element must also produce shear forces (and therefore shear stresses) on the other faces of the element.
Thus, an element experiencing a vertical shear stress also experiences a horizontal shear stress. This is known as the complementary property of shear. This effect can be seen by forming a ‘beam’ out of a stack of paper and applying a vertical force. The pieces of paper slide horizontally relative to each other (Figure 10.6).
Another example is a wooden beam that fails due to shear. In such beams, cracks tend to appear horizontally even though the applied load is vertical. This is due to horizontal shear stress between the layers of the wood (Figure 10.7).
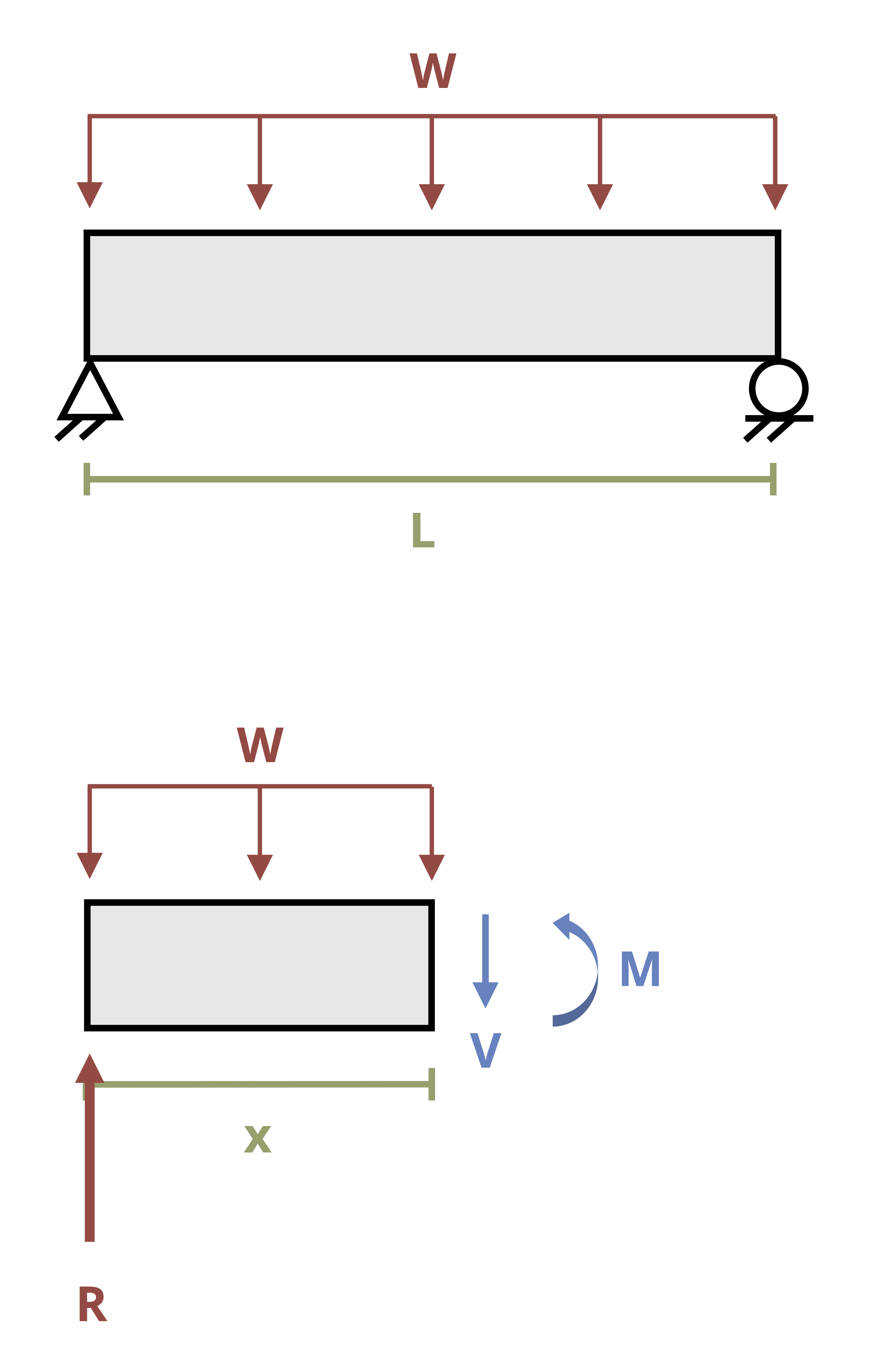
Imagine a beam subjected to an arbitrary vertical load. Consider a small cross-section of width Δx (Figure 10.8). This cross-section is subjected to an external load, an internal shear force on each side of the cross-section, and an internal bending moment on each side of the cross-section. The two shear forces and two bending moments are not necessarily equal.
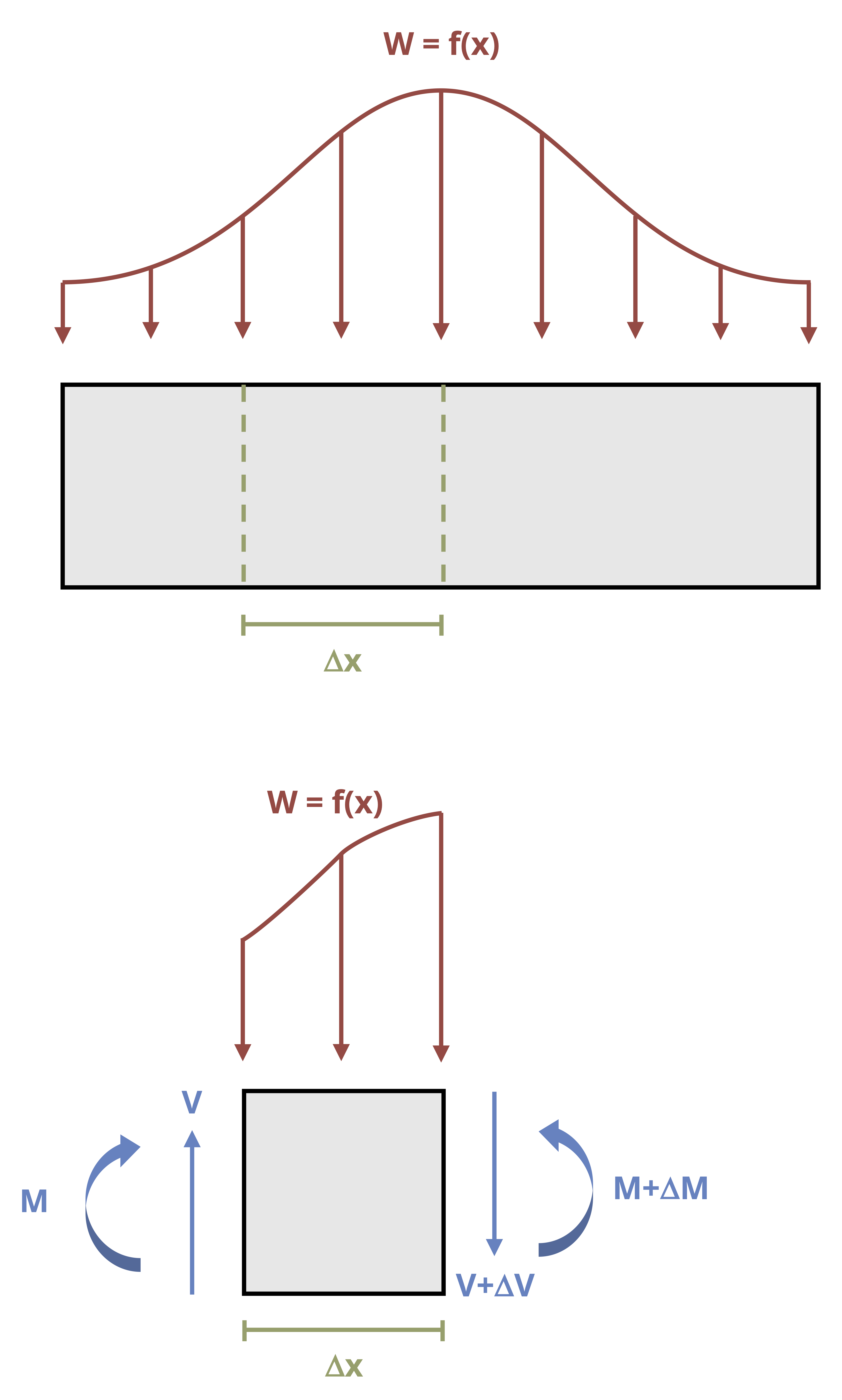
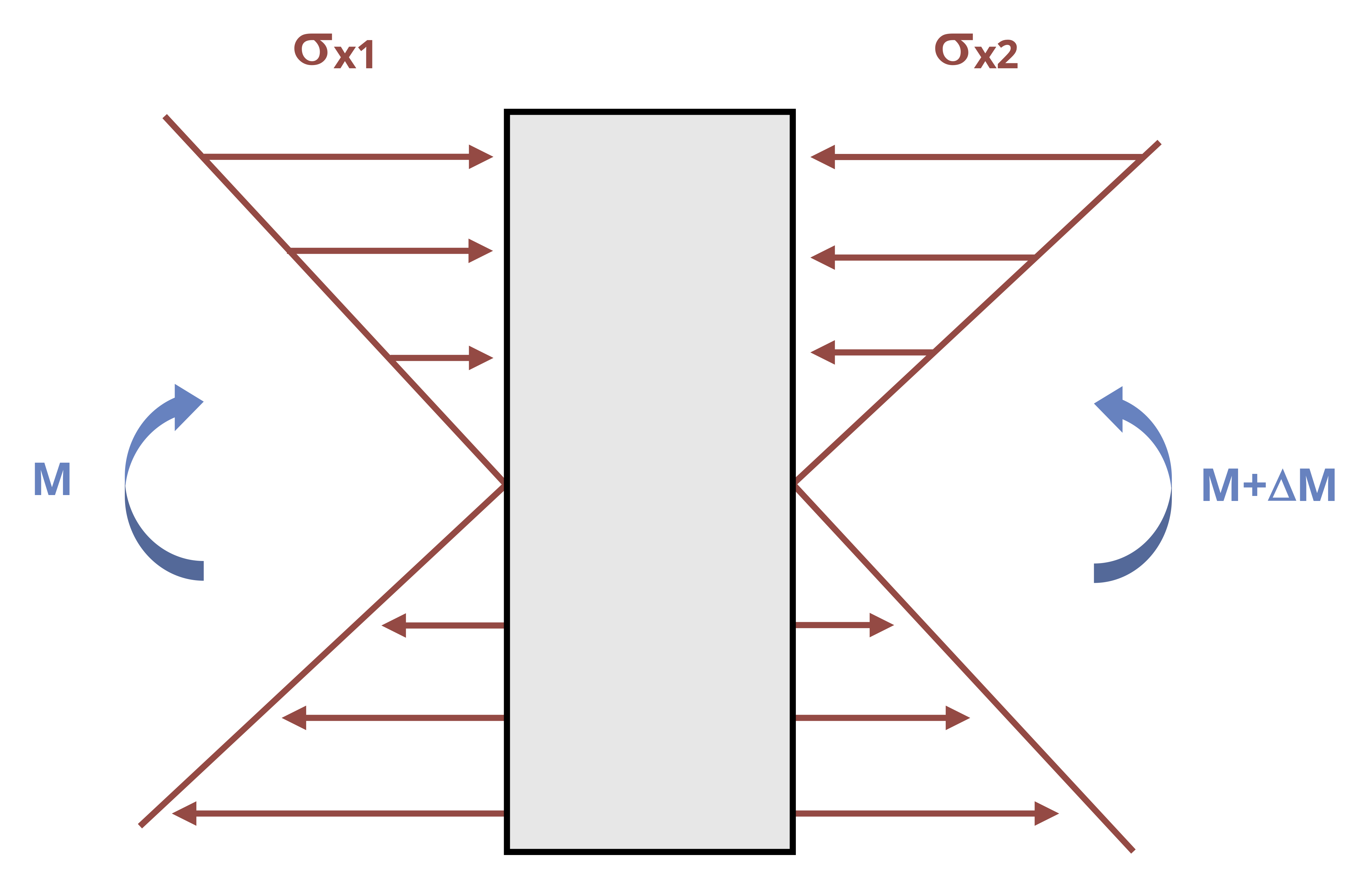
By considering horizontal equilibrium, we do not need to account for the vertical loads (V, V + ΔV, and w). The bending moments (M and M + ΔM) will create horizontal stresses (Figure 10.9) equal to
\[ \sigma_{x 1}=\frac{M y}{I} \]
and
\[ \sigma_{x 2}=\frac{(M+\Delta M) y}{I} \]
Since \(F=\sigma A\), we can determine the total force applied by each bending moment:
\[ F_1=\int \frac{M y}{I} d A \]
and
\[ F_2=\int \frac{(M+\Delta M) y}{I} d A \]
Each force is tensile in part of the beam and compressive in part of the beam. When calculated across the entire cross-section these forces will sum to zero. However, if we consider only part of the cross-section the forces do not sum to zero (Figure 10.10). For the beam to be in equilibrium, there must be a horizontal shear force. For now we’ll call this force F’ and derive an equation for the shear stress it creates.
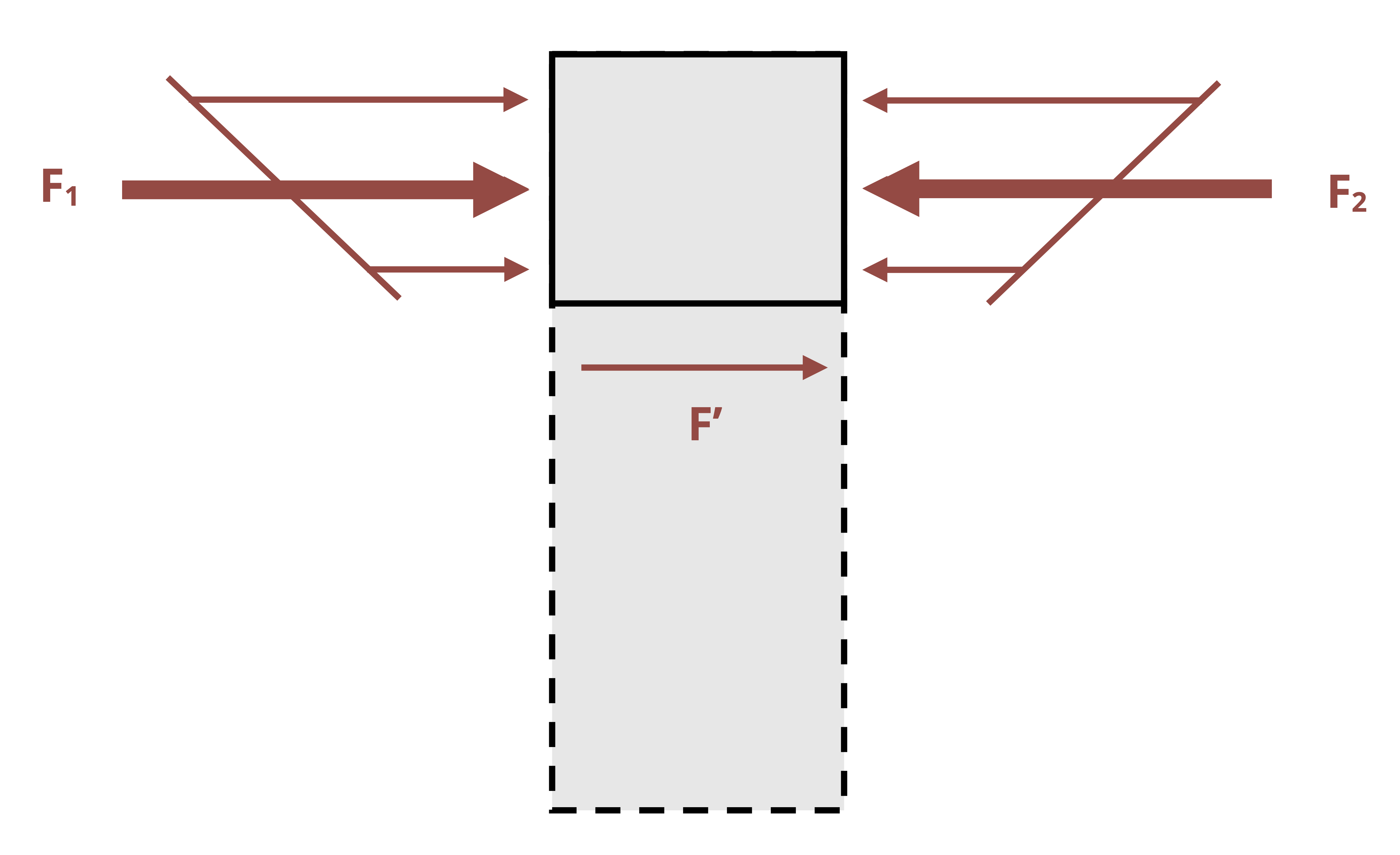
By equilibrium:
\[ \begin{aligned} & \sum F_x=F^{\prime}+\int \frac{M y}{I} d A-\int \frac{(M+\Delta M) y}{I} d A=0 \\ & F^{\prime}=-\int \frac{M y}{I} d A+\int \frac{M y}{I} d A+\int \frac{\Delta M y}{I} d A \\ & F^{\prime}=\int \frac{\Delta M y}{I} d A=\frac{\Delta M}{I} \int y d A \end{aligned} \]
Once the constants are taken out of the integral, the remaining integral is just the first moment of area, Q.
\[ F^{\prime}=\frac{\Delta M}{I} Q \]
We can calculate the shear stress from \(\tau=\frac{V}{A}\) where V = F’ and A is the area of the cross-section that force F’ acts on. This area will be width, Δx, multiplied by the thickness of the beam, t.
\[ \tau=\frac{V}{A}=\frac{F^{\prime}}{\Delta x t}=\frac{\Delta M Q}{\Delta x I t} \]
From Section 7.2 we know that the change in moment with respect to x is equal to the shear force, V
\[ \frac{\Delta M}{\Delta x}=V \\ \]
\[ \boxed{\tau=\frac{VQ}{It}} \tag{10.2}\]
τ = Shear stress at a point on the cross-section [Pa, psi]
V = Internal shear force at the cross-section [N, lb]
Q = 1st moment of area at the point of interest on the cross-section [m3, in.3]
I = Area moment of inertia of the cross-section [m4, in.4]
t = thickness of the cross-section [m, in.]
This is the shear stress equation, allowing us to calculate the shear stress at any point on a cross-section. This is often more useful than simply calculating the average shear stress across the entire cross-section.
Example 10.3 demonstrates calculation of the maximum shear stress in a simply supported beam with a circular cross-section.
Example 10.4 demonstrates how to calculate the maximum stress is a cross-section of varying thickness.
Example 10.3
A simply supported beam with the circular cross-section shown is subjected to a uniformly distributed load w = 30 kN/m across its entire length L = 8 m. Determine the maximum shear stress that occurs in the beam.
The shear stress can be calculated from \(\tau=\frac{V Q}{I t}\). The maximum shear stress will occur when V and Q are at their maximum values.
The maximum shear force, Vmax, can be found by drawing a shear force diagram. Start with a free body diagram of the beam and use this to sketch the shear force diagram using the graphical method of Section 7.4. The loading and supports are symmetric, so each support will resist half of the applied load.
\[ A=B=\frac{w L}{2}=\frac{30\frac{kN}{m} * 8{~m}}{2}=120{~kN} \]
From the diagram it is apparent that the maximum shear force in the beam, Vmax = 120 kN. This occurs at the supports.
The area moment of inertia for the circular cross-section is given by
\[ I=\frac{\pi}{4} r^4=\frac{\pi}{4}(0.02{~m})^4=1.257 \times 10^{-7}{~m}^4 \]
The maximum first moment of area, Qmax, occurs at the neutral axis of the cross-section. For a circular cross-section it was demonstrated in the text that
\[ Q_{max}=\frac{2}{3}r^3=\frac{2}{3}(0.02{~m})^3=5.33\times10^6{~m}^3 \]
The thickness of the cross-section at the neutral axis is equal to the diameter, t = 0.04 m.
With all of the terms known, we can now calculate the maximum shear stress in the beam.
\[ \tau=\frac{V Q}{I t}=\frac{120,000{~N} * 5.33 \times 10^{-6}{~m}^3}{1.257 \times 10^{-7}{~m}^4 * 0.04{~m}}=127\times10^6\frac{N}{m^2}=127{~MPa} \]
Example 10.4
A beam with the cross-section shown is subjected to an internal shear force of 20 kips. Determine:
- The shear stress at the neutral axis of the cross-section
- The shear stress at the point where the thickness of the cross-section changes
Determine the y-coordinate of the centroid using the method of Section 8.1. We will choose our reference point to be at the bottom of the section.
\[ \begin{aligned} & y_1=2.5{~in.}~,~ A_1=5{~in.}^2 \\ & y_2=7{~in.}~,~ A_2=20{~in.}^2 \\ & \bar{y}=\frac{(2.5{~in.} * 5{~in.}^2)+(7{~in.} * 20{~in.}^2)}{5{~in.}^2+20{~in.}^2}=6.1{~in.}~~ \text{from the bottom of the section. } \end{aligned} \]
Determine the area moment of inertia of the entire cross-section using the method of Section 8.2
\[ I=\left(\frac{1 * 5^3}{12}+5 *(2.5-6.1)^2\right)+\left(\frac{5 * 4^3}{12}+20 *(7-6.1)^2\right)=118.08{~in.}^4 \]
The shear force at the neutral axis of the cross-section
Draw a line through the point of interest and use the area above this line to calculate the first moment of area.
\[ Q=y A=\frac{2.9{~in.}}{2} *(2.9{~in.} * 5{~in.})=21.025{~in.}^3 \]
The thickness of the cross-section at this point, t = 5 in.
The shear stress at the neutral axis is then given by:
\[ \tau=\frac{V Q}{I t}=\frac{20,000{~lb} * 21.025{~in.}^3}{118.08{~in.}^4 * 5{~in.}}=712{~psi} \]
The shear stress at the point where the thickness of the cross-section changes
Draw a line through the point of interest and use the area above this line to calculate the first moment of area.
\[ Q=y A=0.9{~in.} *(4 {~in.}* 5{~in.})=18{~in.}^3 \]
The thickness of the cross-section at this point, t = 1 in.
The shear stress at this line is then given by:
\[ \tau=\frac{V Q}{I t}=\frac{20,000 {~lb}* 18{~in.}^3}{118.08{~in.}^4 * 1{~in.}}=3,049{~psi} \]
Note that even though the first moment of area is smaller at this axis, the stress is larger because the thickness of the cross-section decreases significantly at this point.
10.3 Shear Flow
Click to expand
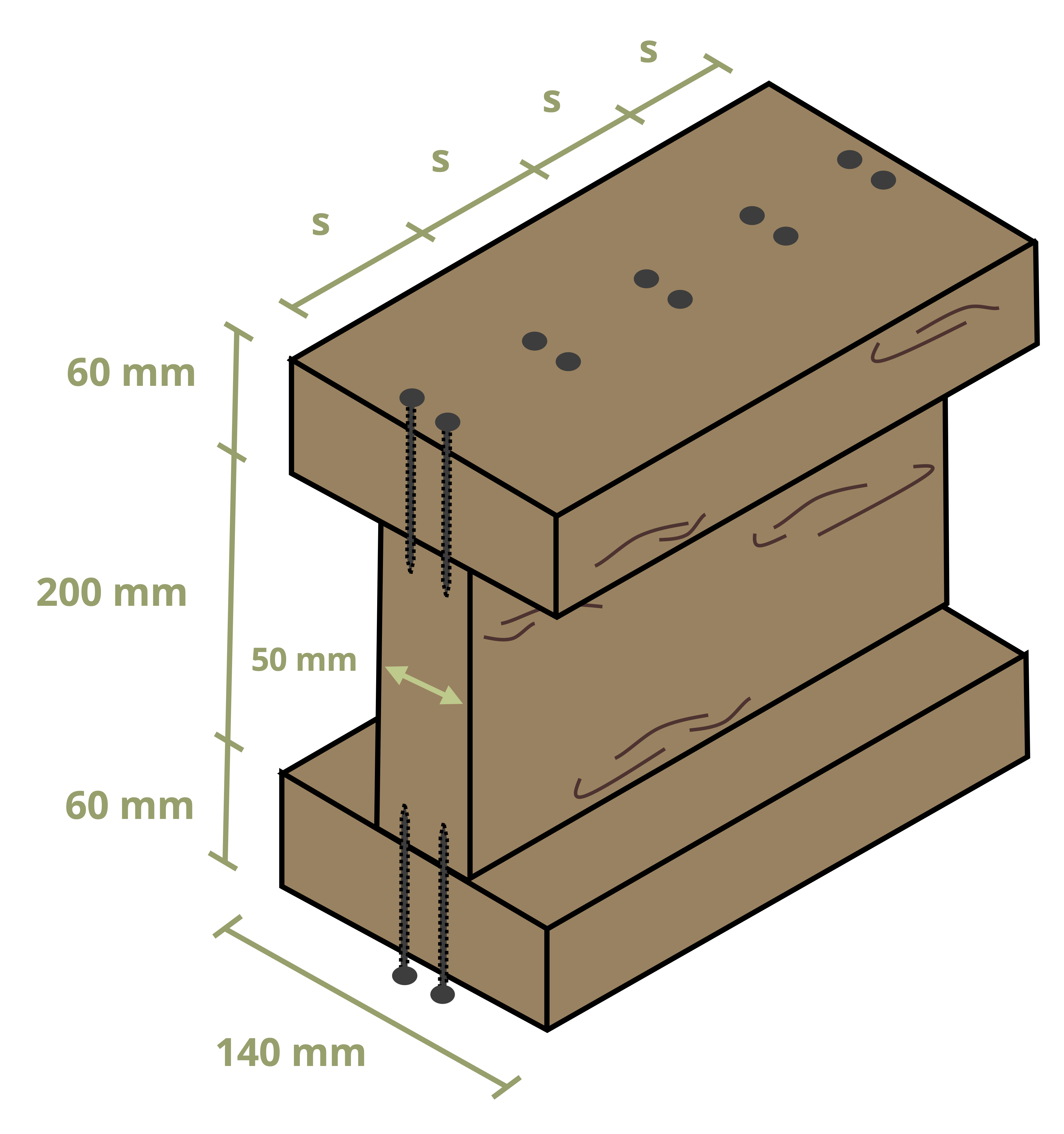
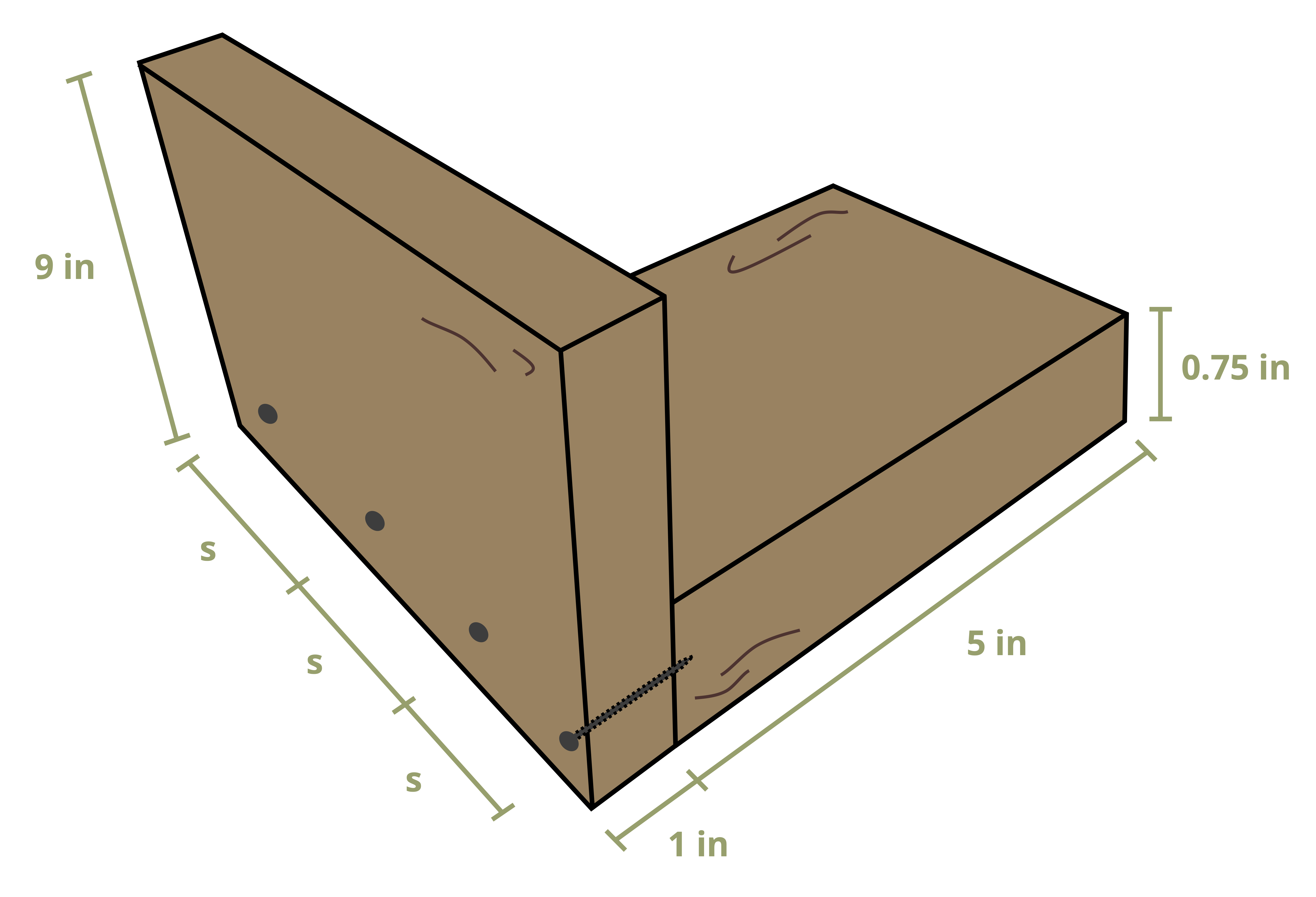
Some cross-sections are formed by connecting multiple pieces together with fasteners such as nails or bolts (Figure 10.11). In such members, we must analyze not only the stresses in the cross-section itself but also the stresses in the fasteners.
A useful quantity in this regard is shear flow, q. Shear flow measures of how much shear force is applied per unit length of the beam, and it is measured in units of force/length [N/m, lb/in.]. For example, if a nail is capable of resisting a shear force up to 10 kN and there is a shear flow of 30 kN/m, it is trivial to determine that we need at least 3 nails for every meter of beam.
Recall from Section 10.2 that the internal horizontal shear force, F’, may be written as
\[ F^{\prime}=\frac{\Delta M}{I} Q \]
Dividing both sides by Δx
\[ \frac{F^{\prime}}{\Delta x}=\frac{\Delta M Q}{\Delta x I} \]
Similar to our derivation in the previous section, we may replace \(\frac{\Delta M}{\Delta x}=V\). We may also replace \(\frac{F^{\prime}}{\Delta x}=q\).
\[ q=\frac{V Q}{I} \]
This equation is very similar to the shear stress equation, but the thickness of the cross-section doesn’t appear here as shear flow is measured per unit length. We will generally want to determine the shear flow at the seam where the individual pieces of the cross-section are joined together as this is where the fasteners must resist the horizontal shear force.
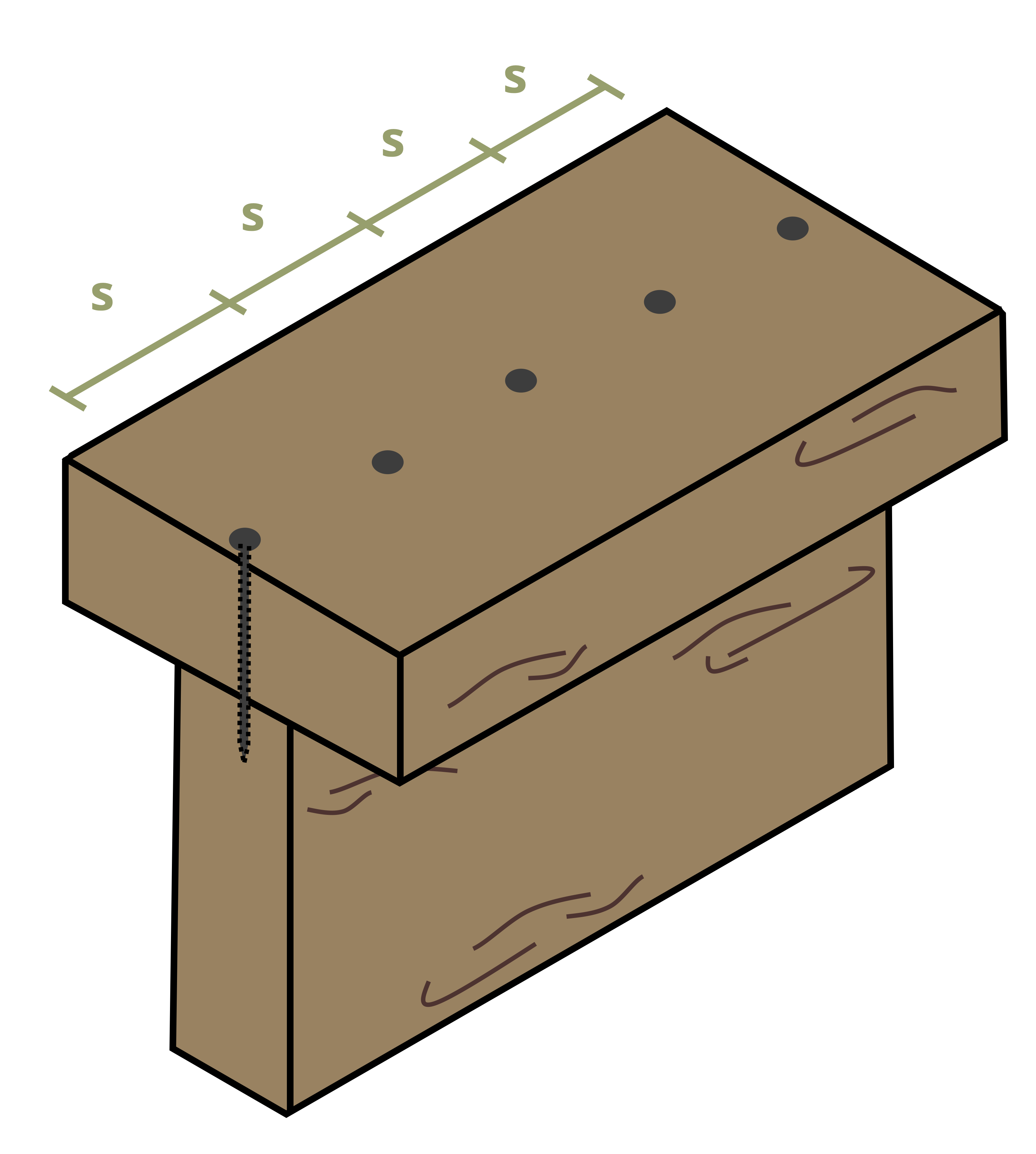
Often we want to determine how far apart we can space the nails along the length of the beam. Since shear flow is the shear force per unit length, if we know how much shear force each fastener can resist, we can say that the shear flow is equal to the force resisted by each fastener (Fnail) divided by the spacing between the fasteners (s). Sometimes there will be multiple rows of nails side-by-side (Figure 10.12). In this case we can multiply the force resisted by each fastener by the number of rows (r).
\[ \boxed{q=\frac{V Q}{I}=\frac{F_{nail} r}{s}} \tag{10.3}\]
q = Shear flow at a line on the cross-section [N/m, lb/in.]
V = Internal shear force at the cross-section [N, lb]
Q = 1st moment of area at the point of interest on the cross-section [m3, in.3]
I = Area moment of inertia of the cross-section [m4, in4]
Fnail = Horizontal shear force resisted by each nail [N, lb]
r = Number of rows of nails resisting the shear force
s = Spacing between nails [m, in.]
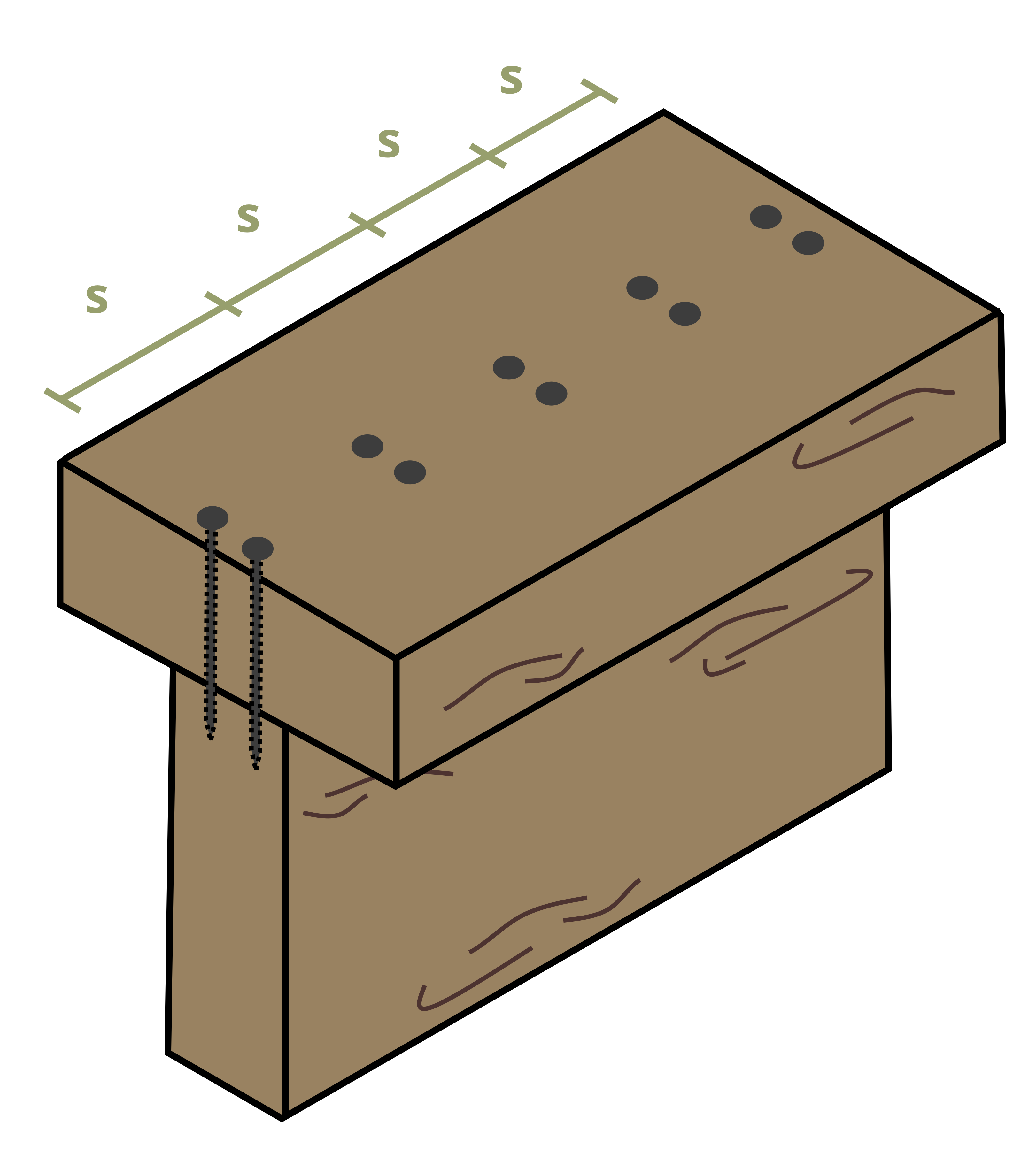
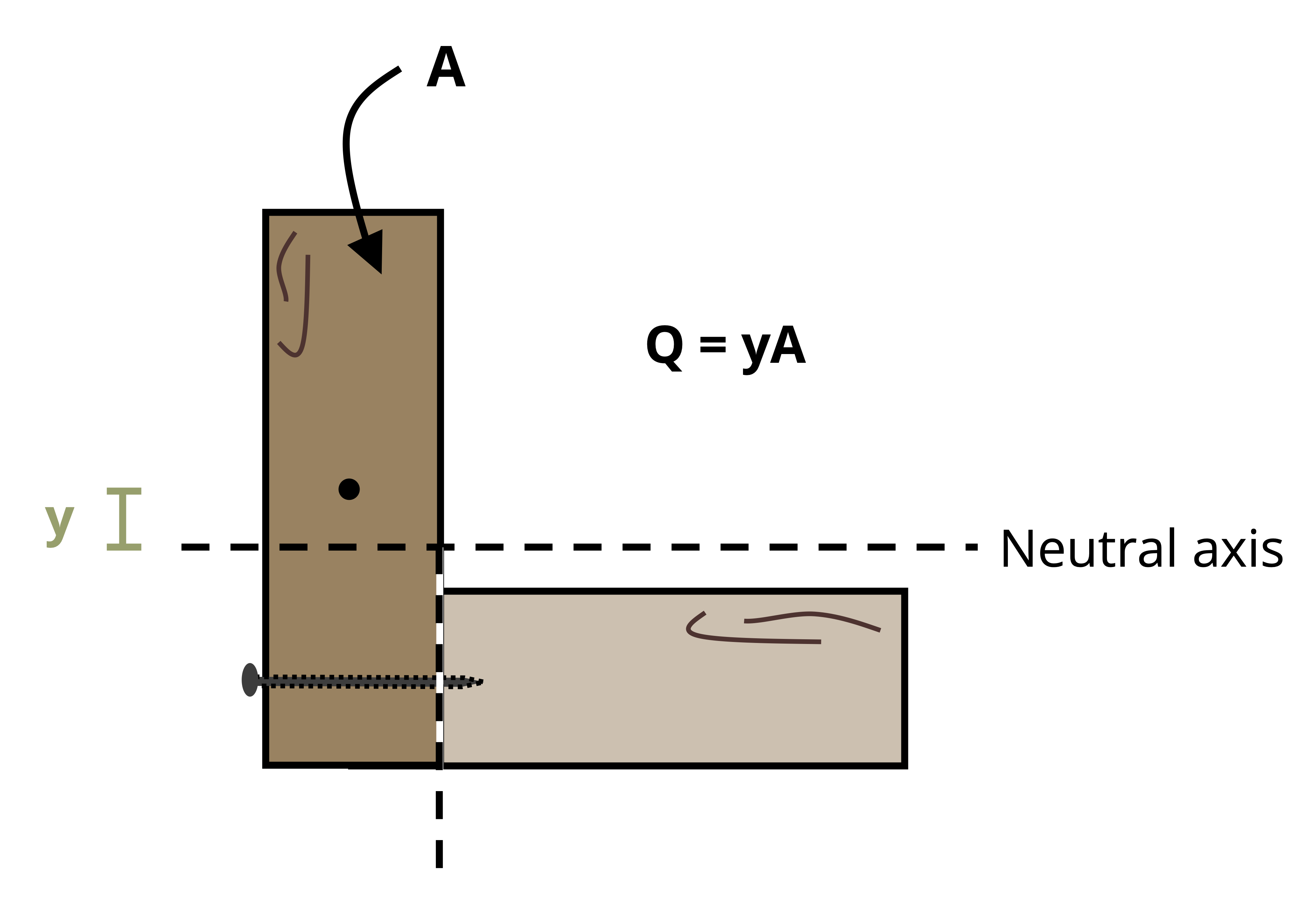
Sometimes fasteners may be placed horizontally (Figure 10.13). In these cases we should still draw a line along the seam perpendicular to the fastener (so vertically in this case). We can then use the area either to the left or right of this line to determine the first moment of area. Note that we still use the vertical distance between the centroid of our chosen area and the neutral axis of the cross-section.
Example 10.5 works through a problem with two rows of nails at each seam.
Example 10.6 involves an L-beam with a horizontal nail.
Example 10.5
A beam is made by nailing together three boards to form the cross-section shown. At each connection, two rows of nails are used to secure the boards. Each nail can resist a horizontal shearing force of 1,500 N. If the beam is subjected to an internal vertical shear force of 4,500 N, determine the minimum required spacing, s, between the rows of nails.
We need to determine the shear flow at one of the points where the beams are connected. Use \(q=\frac{V Q}{I}\) where V = 4,500 N. Since the section is symmetric, we can determine the location of the centroid by inspection, \(\bar{y}=160 \mathrm{~mm}\) from the top and bottom. Now we need to determine the area moment of inertia, I, for the cross-section.
By considering the area as a large rectangle with two smaller rectangles cut out:
\[ I=\frac{140 * 320^3}{12}-2\left(\frac{45 * 200^3}{12}\right)=322.3 \times 10^6{~mm}^4=322.3 \times 10^{-6}{~m}^4 \]
Next draw a line through the point of interest (along the seam where the nails are holding the boards together) and determine the first moment of area, Q, at this line.
\[ Q=y A=130{~mm} *(60{~mm} * 140{~mm})=1092 \times 10^3{~mm}^3=1,092 \times 10^{-6}{~m}^3 \]
Shear flow:
\[ q=\frac{V Q}{I}=\frac{4500 {~N}* 1092 \times 10^{-6}{~m}^3}{322.3 \times 10^{-6}{~m}^4}=15,247~\frac{N}{m} \]
Finally, set the shear flow, \(q=\frac{F_{nail} r}{s}\), and solve for the spacing, s:
\[ s=\frac{F_{nail} r}{q}=\frac{1500{~N} * 2}{15247~\frac{N}{m}}=0.197 \mathrm{~m}=197 \mathrm{~mm} \]
Example 10.6
A beam is formed by nailing two boards together to form the L-shaped cross-section shown. The nails are spaced a distance s = 1.5 in. apart along the length of the beam and each nail can resist a force of 700 lb in shear. Determine the maximum allowable internal shear force in the beam.
Determine the allowable shear flow in the beam based on the nails.
\[ q=\frac{F_{nail} r}{s}=\frac{700{~lb} * 1}{1.5{~in.}}=467~\frac{lb}{in.} \]
This shear flow can be set equal to \(q=\frac{V Q}{I}=467~\frac{lb}{in.}\)
Find the y-coordinate of the centroid of the cross-section, setting the reference point at the bottom of the section.
\[ \begin{aligned} & y_1=0.375{~in.}~,~ A_1=5{~in.} * 0.75{~in.}=3.75{~in.}^2 \\ & y_2=4.5{~in.}~,~ A_2=1{~in.} * 9{~in.}=9{~in}^2 \\ & \bar{y}=\frac{(0.375{~in.} * 3.75{~in.}^2)+(4.5{~in.} * 9{~in.}^2)}{3.75{~in.^2}+9{~in.^2}} = 3.287{~in.}~~\text{from the bottom of the section} \end{aligned} \]
Find the area moment of inertia for the entire cross-section.
\[ I=\left(\frac{5 * 0.75^3}{12}+3.75 *(3.287-0.375)^2\right)+\left(\frac{1 * 9^3}{12}+9 *(4.5-3.287)^2\right)=106{~in.}^4 \]
Draw a line along the seam where the nails are holding the two boards together. Note that this is a vertical line. To determine the first moment of area, Q, we use the area to either the left side or the right side of this line. Note that when calculating Q=yA, the distance y is still measured in the vertical direction between the centroid of area A and the neutral axis of the cross-section.
\[ \begin{aligned} & y=4.5{~in.}-3.287{~in.}=1.213{~in.} \\ & A=(1{~in.} * 9{~in.})=9{~in.}^2 \\ & Q=1.213{~in.} * 9{~in.^2}=10.9{~in.}^3 \end{aligned} \]
Finally, solve for the maximum allowable internal shear force in the beam by rearranging the shear flow equation.
\[ V=\frac{q I}{Q}=\frac{467~\frac{lb}{in.} * 106{~in.^4}}{10.9{~in.^3}}=4,541{~lb} \]